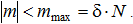Сопротивление, возникающее при стремлении сдвинуть одно тело по поверхности другого, называется трением скольжения. Возникновение трения обусловлено, прежде всего, шероховатостью соприкасающихся тел. Изучение всех факторов, влияющих на трение, представляет собой весьма сложную физико-механическую проблему, рассмотрение которой выходит за рамки курса теоретической механики.
7.1. Законы трения скольжения
В инженерных расчетах обычно исходят из установленных опытным путем закономерностей, называемых законами трения скольжения.
При стремлении сдвинуть одно тело по поверхности другого в плоскости соприкосновения тел возникает сила трения, которая может принимать любые значения отличные от нуля до величины предельной силы трения 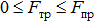 .
.
Предельная сила трения численно равна произведению статического коэффициента трения 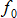 на нормальное давление или нормальную реакцию
на нормальное давление или нормальную реакцию 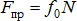 .
.
Значение предельной силы трения в достаточно широких пределах не зависит от площади соприкосновения при трении поверхностей.
Следует отметить, что величине 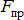 сила трения будет равна лишь тогда, когда действующая на тело сдвигающая сила достигнет такого значения, что при малейшем ее увеличении тело начнет двигаться (скользить). Равновесие, имеющее место, когда сила трения равна
сила трения будет равна лишь тогда, когда действующая на тело сдвигающая сила достигнет такого значения, что при малейшем ее увеличении тело начнет двигаться (скользить). Равновесие, имеющее место, когда сила трения равна 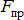 , будем называть предельным равновесием.
, будем называть предельным равновесием.
7.2. Реакция шероховатой поверхности. Угол трения. Конус трения
Рассмотрим тело весом 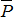 , лежащее на горизонтальной шероховатой плоскости. Пусть к телу приложена горизонтальная сила
, лежащее на горизонтальной шероховатой плоскости. Пусть к телу приложена горизонтальная сила 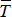 , под действием которой тело находится в покое. В этом случае сила
, под действием которой тело находится в покое. В этом случае сила 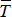 должна уравновешиваться другой силой, равной по величине и направленной в противоположную сторону – силой трения скольжения (рис. 7.1).
должна уравновешиваться другой силой, равной по величине и направленной в противоположную сторону – силой трения скольжения (рис. 7.1).
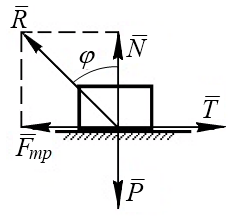
Рис. 7.1
Следовательно, полная реакция шероховатой поверхности слагается из двух составляющих: нормальной реакции 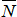 и перпендикулярной ей силы трения
и перпендикулярной ей силы трения 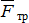 . При увеличении силы трения от нуля до
. При увеличении силы трения от нуля до 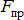 полная реакция шероховатой поверхности изменится от
полная реакция шероховатой поверхности изменится от 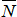 до
до 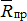 , а угол
, а угол 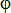 от нуля до
от нуля до 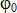 . Наибольший угол
. Наибольший угол 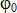 , который полная реакция шероховатой поверхности образует с нормалью, называется углом трения (рис.7.2а).
, который полная реакция шероховатой поверхности образует с нормалью, называется углом трения (рис.7.2а).
Если вектор полной реакции шероховатой поверхности 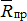 поворачивать вокруг нормали, то он опишет поверхность конуса (рис.7.2б), называемого конусом трения. Построив конус трения, можно определить равновесие тела. Для равновесия тела, лежащего на шероховатой поверхности, необходимо и достаточно, чтобы действующая на тело сила проходила внутри конуса трения (или по его образующей через вершину конуса).
поворачивать вокруг нормали, то он опишет поверхность конуса (рис.7.2б), называемого конусом трения. Построив конус трения, можно определить равновесие тела. Для равновесия тела, лежащего на шероховатой поверхности, необходимо и достаточно, чтобы действующая на тело сила проходила внутри конуса трения (или по его образующей через вершину конуса).

Рис. 7.2
Если к телу, лежащему на шероховатой поверхности, приложить силу 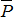 , образующую угол α с нормалью (рис. 7.3), то тело сдвинется только в том случае, когда сдвигающее усилие будет больше предельной величины трения
, образующую угол α с нормалью (рис. 7.3), то тело сдвинется только в том случае, когда сдвигающее усилие будет больше предельной величины трения 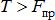 .
.
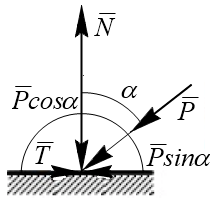
Рис. 7.3
Поскольку 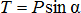 и
и 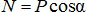 , то
, то 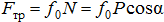 . Условием сдвига является неравенство
. Условием сдвига является неравенство 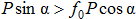 или
или 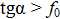 , т.к.
, т.к. 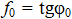 , то
, то 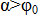 . Следовательно, никакой силой, образующей с нормалью угол
. Следовательно, никакой силой, образующей с нормалью угол 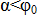 , невозможно сдвинуть тело. Это условие объясняет известное в инженерной практике явление заклинивания и самоторможение тел.
, невозможно сдвинуть тело. Это условие объясняет известное в инженерной практике явление заклинивания и самоторможение тел.
7.3. Методические указания по исследованию условий равновесия тел при наличии трения
Исследование равновесия тел с учетом трения сводится к рассмотрению предельных положений равновесия.
1. Выделяем тело (систему тел), равновесие которого следует рассмотреть.
2. Расставляем все активные силы, действующие на твердое тело (систему тел).
3. Изображаем систему координат.
4. Освобождаем тело от связей, заменяя их действие силами реакций. Реакцию шероховатой поверхности представляетм в виде нормальной реакции 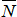 и силы трения
и силы трения 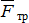 .
.
5. Составляем уравнения равновесия для выделенного тела (системы тел).
6. Решая полученную систему уравнений, определяем искомые величины.
Пример. Однородная лестница АВ весом Р опирается своим нижним концом на горизонтальный шероховатый пол, а верхним концом – на шероховатую вертикальную стену. Коэффициент трения лестницы о пол и стену одинаков и равен 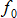 . Определить реакции пола NA и стены NB, а так же наибольший угол α, составляемый между стеной и лестницей в положении равновесия (рис. 7.4).
. Определить реакции пола NA и стены NB, а так же наибольший угол α, составляемый между стеной и лестницей в положении равновесия (рис. 7.4).
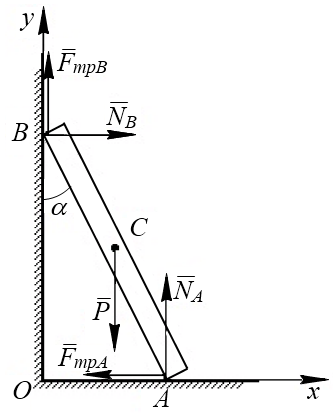
Рис. 7.4
Решение. Исследование равновесия тел с учетом сил трения сводится к рассмотрению предельных положений равновесия.
Так, при исследовании равновесия лестницы АВ, опирающейся на негладкие пол и стену, следует считать угол наклона α предельным, при его увеличении равновесие лестницы нарушится.
Покажем на схеме действующие на лестницу силы и составим уравнения равновесия сил (рис. 7.4):
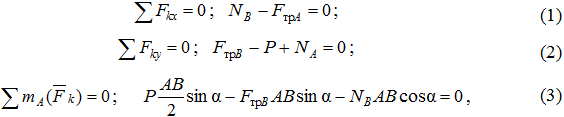
где 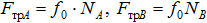
Из уравнения (1): 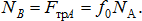
Из уравнения (2): 
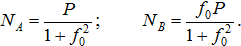
Из уравнения (3): 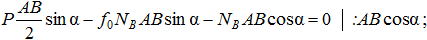
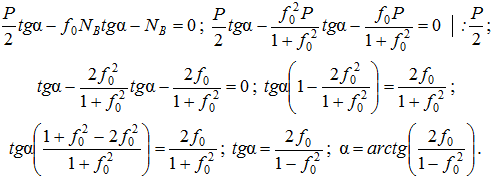
Ответ: для того, чтобы лестница была в равновесии необходимо, чтобы угол наклона к стене не превышал угол 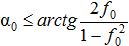 .
.
7.4. Равновесие твердого тела при наличии трения качения
Если рассматриваемое тело имеет форму катка и под действием приложенных активных сил может катиться по поверхности другого тела, то из-за деформации поверхностей этих тел в месте соприкосновения могут возникнуть силы реакции, препятствующие не только скольжению, но и качению. Примерами таких катков являются различные колеса, как, например, у электровозов, вагонов, автомашин, шарики и ролики в шариковых и роликовых подшипниках и т.п.
Пусть цилиндрический каток находится на горизонтальной плоскости под действием активных сил. Соприкосновение катка с плоскостью из-за деформации фактически происходит не вдоль одной образующей, как в случае абсолютно твердых тел, а по некоторой площадке. Если активные силы приложены симметрично относительно среднего сечения катка, то есть вызывают одинаковые деформации вдоль всей его образующей, то можно изучать только одно среднее сечение катка. Этот случай рассмотрен ниже.
Между катком и плоскостью, на которой он покоится, возникают силы трения, если приложить к оси катка силу 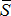 (рис. 7.5), стремящуюся его двигать по плоскости.
(рис. 7.5), стремящуюся его двигать по плоскости.
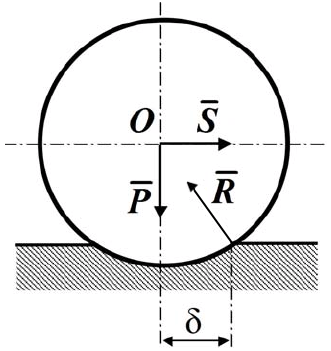
Рис. 7.5
Рассмотрим случай, когда сила 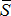 параллельна горизонтальной плоскости. Из опыта известно, что при изменении модуля силы
параллельна горизонтальной плоскости. Из опыта известно, что при изменении модуля силы 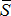 от нуля до некоторого предельного значения
от нуля до некоторого предельного значения 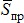 каток остается в покое, т.е. силы, действующие на каток, уравновешиваются. Кроме активных сил (веса
каток остается в покое, т.е. силы, действующие на каток, уравновешиваются. Кроме активных сил (веса 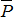 и силы
и силы 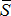 ), к катку, равновесие которого рассматривается, приложена реакция плоскости. Из условия равновесия трех непараллельных сил следует, что реакция плоскости
), к катку, равновесие которого рассматривается, приложена реакция плоскости. Из условия равновесия трех непараллельных сил следует, что реакция плоскости 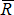 должна проходить через центр катка О, так как две другие силы приложены к этой точке.
должна проходить через центр катка О, так как две другие силы приложены к этой точке.
Следовательно, точка приложения реакции С должна быть смещена на некоторое расстояние δ от вертикали, проходящей через центр колеса, иначе реакция 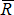 не будет иметь горизонтальной составляющей, необходимой для удовлетворения условий равновесия. Разложим реакцию плоскости
не будет иметь горизонтальной составляющей, необходимой для удовлетворения условий равновесия. Разложим реакцию плоскости 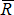 на две составляющие: нормальную составляющую
на две составляющие: нормальную составляющую 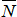 и касательную реакцию
и касательную реакцию 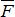 , являющуюся силой трения (рис. 7.6).
, являющуюся силой трения (рис. 7.6).
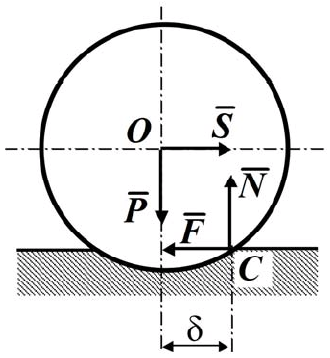
Рис. 7.6
В предельном положении равновесия катка к нему будут приложены две взаимно уравновешивающиеся пары: одна пара сил 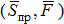 с моментом
с моментом 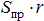 (где r – радиус катка) и вторая пара сил
(где r – радиус катка) и вторая пара сил 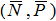 , удерживающая каток в равновесии.
, удерживающая каток в равновесии.
Момент пары, называемой моментом трения качения, определяется формулой:

Из (1) следует, что для того, чтобы имело место чистое качение (без скольжения), необходимо, чтобы сила трения качения 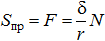 была меньше максимальной силы трения скольжения:
была меньше максимальной силы трения скольжения:

где f – коэффициент трения скольжения.
Таким образом, чистое качение (без скольжения) будет, если 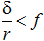 .
.
Трение качения возникает из-за деформации катка и плоскости, вследствие чего соприкосновение между катком и плоскостью происходит по некоторой поверхности, смещенной от нижней точки катка в сторону возможного движения.
Если сила 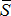 не направлена по горизонтали, то ее следует разложить на две составляющие, направленные по горизонтали и вертикали. Вертикальную составляющую следует сложить с силой
не направлена по горизонтали, то ее следует разложить на две составляющие, направленные по горизонтали и вертикали. Вертикальную составляющую следует сложить с силой 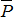 , и мы снова приходим к схеме действия сил, изображенных на рис. 7.6.
, и мы снова приходим к схеме действия сил, изображенных на рис. 7.6.
Установлены следующие приближенные законы для наибольшего момента пары сил, препятствующей качению:
1. Наибольший момент пары сил, препятствующий качению, в довольно широких пределах не зависит от радиуса катка.
1. Предельное значение момента 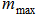 пропорционально нормальному давлению и равной ему нормальной реакции
пропорционально нормальному давлению и равной ему нормальной реакции 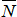 :
: 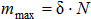 .
.
Коэффициент пропорциональности δ называют коэффициентом трения качения при покое или коэффициентом трения второго рода. Коэффициент δ имеет размерность длины.
3. Коэффициент трения качения δ зависит от материала катка, плоскости и физического состояния их поверхностей. Коэффициент трения при качении в первом приближении можно считать не зависящим от угловой скорости качения катка и его скорости скольжения по плоскости. Для случая качения вагонного колеса по стальному рельсу коэффициент трения качения δ=0.5мм.
Законы трения качения, как и законы трения скольжения, справедливы для не очень больших нормальных давлений и не слишком легко деформирующихся материалов катка и плоскости.
Эти законы позволяют не рассматривать деформации катка и плоскости, считая их абсолютно твердыми телами, касающимися в одной точке. В этой точке соприкосновения кроме нормальной реакции и силы трения надо приложить еще и пару сил, препятствующую качению.
Для того, чтобы каток не скользил, необходимо выполнение условия
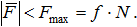
Для того чтобы каток не катился, должно выполняться условие