5.1. Момент силы относительно оси
Рассмотрим тело, к которому в точке А приложена сила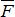 
. Проведём через точку А плоскость xy. Разложим силу 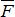на составляющие: одну параллельно оси z и другую, лежащую в плоскости xy - 
. Проведём ось z. Точку пересечения оси z с плоскостью xy обозначим буквой О. Сила 
, параллельная оси z, не обладает вращательным эффектом; она только может переместить тело вдоль оси z (рис. 5.1).
Вращательный эффект силы 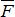может создавать составляющая 
, следовательно, момент силы относительно оси равен моменту проекции этой силы на плоскость, перпендикулярную оси, взятому относительно точки пересечения оси с плоскостью (рис. 5.1).
Рис. 5.1
Момент силы относительно оси равен нулю, если сила параллельна оси или когда сила пересекает ось, относительно которой определяется момент силы. Обобщая эти условия, можно заключить, что момент силы относительно оси равен нулю, когда сила и ось находятся в одной плоскости.
Для вычисления момент силы относительно оси z необходимо:
1) провести плоскость xy, перпендикулярную этой оси;
2) спроецировать на эту плоскость силу 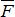и найти величину проекции ;
3) опустить из точки О перпендикуляр на линию действия силы и найти длину перпендикуляра h;
4) вычислить величину момента силы 
;
5) определить знак момента силы.
Таким образом, модуль момента силы 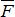относительно оси z (рис. 5.1) равен: 
.
Момент силы 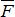относительно оси z будет иметь знак «плюс», когда с положительного конца оси поворот, который стремится совершить сила , будет виден происходящим против хода часовой стрелки, и знак «минус», когда по ходу часовой стрелки.
5.2. Теорема Вариньона для моментов силы относительно оси. Аналитические формулы для моментов силы относительно координатных осей
Для пространственной системы сходящихся сил справедлива теорема Вариньона, приведенная во второй главе (п. 2.3.6): 
. Момент равнодействующей силы относительно точки равен векторной сумме моментов всех сил системы относительно той же точки. Если обе части векторного равенства спроецировать на ось z, проходящую через центр О, то получим: 
. Полученная формула есть теорема Вариньона относительно оси.
Разложим пространственную силу 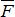, приложенную в точке А с координатами x, y, z, на составляющие 
, 
и (рис.5.2). Тогда по теореме Вариньона: 
. Так как по свойству момента силы 
, то получим: 
.
Рис. 5.2
Аналогично находятся моменты относительно осей y и z. Окончательно, получим:
Полученные формулы есть аналитические формулы для моментов силы относительно координатных осей.
5.3. Приведение произвольной пространственной системы сил к данному центру
Произвольная пространственная система сил, действующих на абсолютно твердое тело, при приведении к произвольно выбранному центру О заменяется одной силой 
, равной главному вектору системы сил и приложенной в центре приведения О, и одной парой с моментом 
, равным главному моменту системы сил относительно центра О. Доказательство данного утверждения аналогично рассмотренному во второй главе (п. 2.5). Однако, в случае приведения пространственной системы сил, учитываем, что главный вектор и главный момент не лежат в одной плоскости.
5.4. Приведение пространственной системы сил к простейшему виду
Частные случаи приведения пространственной системы сил приведены в табл. 5.1.
Таблица 5.1
Частные случаи приведения пространственной системы сил
|
№
|
Значения главного вектора и главного момента
|
Результат приведения
|
|
1
|
|
Система сил приводится к паре сил, момент которой равен главному моменту  (главный момент системы сил не зависит от выбора центра приведения О).
|
|
2
|
|
Система сил приводится к равнодействующей, равной , проходящей через центр О.
|
|
3
|
|
Система сил приводится к равнодействующей  , равной главному вектору и параллельной ему и отстоит от него на расстоянии  . Положение линии действия равнодействующей должно быть таким, чтобы направление ее момента относительно центра приведения О совпадало с направлением относительно центра О.
|
|
4
|
 , причем векторы и не перпендикулярны
|
Система сил приводится к динаме (силовому винту) – совокупности силы и пары сил, лежащей в плоскости, перпендикулярной к этой силе.
|
|
5
|
|
Система сил, приложенных к твердому телу, является уравновешивающейся.
|
5.5. Равновесие произвольной пространственной системы сил
Для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из трех координатных осей и суммы их моментов относительно этих осей были равны нулю:
В том случае, если система сил образует пространственную систему параллельных сил, то оси координат целесообразно выбрать так, чтобы одна из осей была параллельна силам. В этом случае число уравнений равновесия будет равно трём. Например, если система сил параллельна оси z:
5.6. Методические указания к решению задач по исследованию условий равновесия тела, находящегося под действием произвольной пространственной системы сил
Порядок решения задач
1. Выделить материальную систему (тело), равновесие которой следует рассмотреть.
2. Приложить к выделенному телу все активные (заданные) силы.
3. Освободить тело от связей, приложив соответствующие реакции.
4. Направить оси координат.
5. Составить уравнения равновесия произвольной пространственной системы сил, из которых определить искомые величины.
Если в результате решения искомая реакция получается положительной, то это значит, что направление ее выбрано верно, если отрицательной, то направление реакции противоположно выбранному (модуль ее при этом остается прежним).
После того, как задача решена, необходимо произвести проверку правильности решения. Для этого следует составить сумму моментов относительно трех новых взаимно перпендикулярных осей, при этом необходимо учитывать уже исправленные направления реакций. Равенство нулю суммы моментов подтвердит правильность решения задачи.
Пример. Однородная прямоугольная пластинка весом Р = 60Н прикреплена к стене при помощи шарового шарнира А и цилиндрического шарнира В. Пластинка удерживается в горизонтальном положении тросом СЕ, наклоненному к горизонтальной плоскости под углом 30°. Определить натяжение троса и опорные реакции.
Решение.
1) Рассмотрим равновесие пластинки АВСD, т.е. объектом исследовании задачи является данная пластинка (рис. 5.3).
2) Приложим к пластинке заданную силу тяжести 
в точке пересечения диагоналей пластинки;
3) Освободим тело от наложенных на него связей (в точке А – шаровой шарнир, в точке B – цилиндрический шарнир и в точке C – нить). Реакцию шарового шарнира разложим на три составляющие 
, цилиндрического шарнира – на две составляющие 
(в плоскости, перпендикулярной оси цилиндрического шарнира); реакцию нити 
направим вдоль нити от точки C к точке E.
Рис.5.3
4) Для определения величин шести неизвестных реакций связей 
составим 6 уравнений равновесия действующей на пластинку произвольной пространственной системы сил. Переходя к составлению уравнений равновесия, заметим, что неизвестны углы, которые образует сила с осями x и y, поэтому разложим силу на две составляющие, чтобы одна из них, 
, лежала в плоскости xy пластинки, а вторая, 
, была параллельна оси z, т.е. 
. Модули этих составляющих равны: 
; 
. Затем составляющую разложим по осям координат x и y: 
, 
.
Составим уравнения равновесия данной системы:
Из уравнения (6): 
Из уравнения (5): 
Отсюда: 
Из уравнения (1): 
Из уравнения (2): 
Из уравнения (4): 
Из уравнения (3): 
Проверка:
Уравнение моментов относительно оси x1:
Уравнение моментов относительно оси y1:
Уравнение моментов относительно оси z1:
Проверка сошлась.
Ответ:
Пример. Две однородные прямоугольные плиты жестко соединены под прямым углом друг к другу и закреплены сферическим шарниром в точке A, цилиндрическим шарниром в точке B, а также невесомым стержнем 1 (рис. 5.4). Размеры плит указаны на рисунке. Определить реакции связей, если известно, что веса плит равны Р1=5 кН; Р2=3кН; момент пары сил равен М=4 кН м; а=0,6 м; модули заданных сил F3=10 кН; F4=12 кН; α3=60°, силы 
, 
приложены к серединам стороны плиты.
Рис. 5.4
Решение.
1) Рассмотрим равновесие плиты. Объект исследования – плита (рис. 5.4).
2) На плиту действуют заданные силы , , пара сил с моментом М, вес обеих плит.
3) Связи: А – сферический шарнир, В – цилиндрический шарнир (подшипник), 1 – стержень. Реакцию сферического шарнира А разложим на три составляющие 
, цилиндрического (подшипника) – на две составляющие 
(в плоскости, перпендикулярной оси подшипника); реакцию 
стержня 1 направим вдоль стержня 1 (считаем, что он сжат).
4) Для определения шести неизвестных реакций 
составим шесть уравнений равновесия действующей на плиту пространственной системы сил:
5) Подставим числовые значения всех заданных величин и, решив полученную систему уравнений, найдем искомые реакции:
