2.1. Система параллельных сил. Сложение двух параллельных сил
Сложение параллельных сил геометрическим способом по правилу параллелограмма сил не представляется возможным. Для решения поставленной задачи используем метод приведения параллельных сил к сходящимся силам.
Пусть на тело действуют две параллельные силы 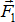 и
и 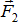 (рис.2.1).
(рис.2.1).
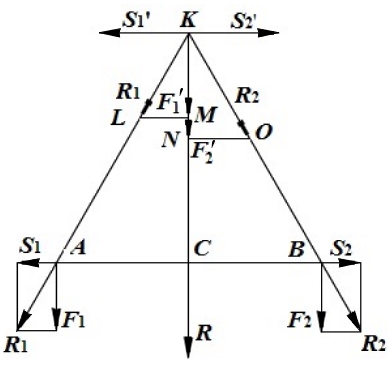
Рис.2.1
Приложим к телу в точках А и В две равные по величине, но противоположные по направлению силы  и
и 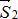 и сложим их с заданными силами
и сложим их с заданными силами 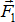 и
и 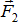 , получим равнодействующие этих сил
, получим равнодействующие этих сил 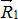 и
и 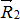 . Эти силы непараллельны и лежат в одной плоскости. Следовательно, они пересекаются в одной точке. Переносим эти силы
. Эти силы непараллельны и лежат в одной плоскости. Следовательно, они пересекаются в одной точке. Переносим эти силы 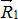 и
и 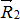 вдоль линии их действия и приложим их к точке К.
вдоль линии их действия и приложим их к точке К.
Далее, разложим эти силы на составляющие 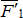 ,
, 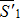 и
и 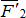 ,
, 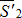 . Силы
. Силы 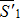 и
и 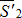 можно отбросить как уравновешенные силы. Следовательно на тело к точке К будут действовать только две силы
можно отбросить как уравновешенные силы. Следовательно на тело к точке К будут действовать только две силы 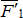 и
и 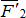 , которые по величине равны силам
, которые по величине равны силам 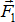 и
и 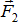 . Сумма сил
. Сумма сил 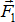 и
и 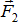 (равнодействующая
(равнодействующая 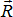 ) направлена вдоль одной прямой:
) направлена вдоль одной прямой: 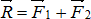 . Из подобия треугольников КСА и КМL и треугольников KCB и KON находим:
. Из подобия треугольников КСА и КМL и треугольников KCB и KON находим: 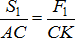 ,
, 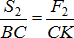 ,
, 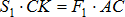 ,
, 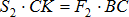 , отсюда
, отсюда 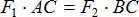 , окончательно:
, окончательно: 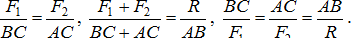
Таким образом, две параллельные силы, направленные в одну сторону, имеют равнодействующую, параллельную им, равную по величине их сумме и направленную в ту же сторону. Линия действия равнодействующей силы расположена между линиями действия заданных сил и делит отрезок прямой между линиями действия этих сил на части, обратно пропорциональные силам.
2.2. Сложение двух параллельных сил, направленных в противоположные стороны
Пусть к телу в точках А и В приложены две параллельные неравные по величине и противоположно направленные силы 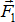 и
и 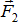 , причем F1>F2 (рис. 2.2). Разложим силу
, причем F1>F2 (рис. 2.2). Разложим силу 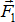 на две составляющие силы, одна из которых равна
на две составляющие силы, одна из которых равна 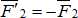 , а вторая
, а вторая 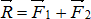 .
.
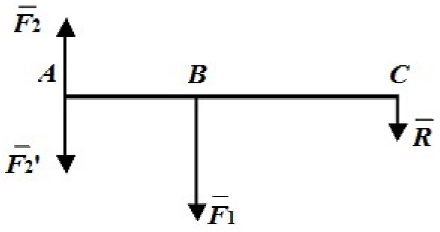
Рис. 2.2
Точку приложения силы 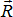 определим, решая задачу о сложении двух параллельных сил
определим, решая задачу о сложении двух параллельных сил 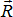 и
и 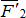 , где их равнодейтсвующая – сила
, где их равнодейтсвующая – сила 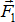 .
.
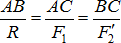
Поскольку 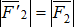 , имеем:
, имеем:
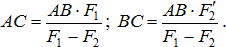
Две неравные параллельные силы, направленные в противоположные стороны, приводятся к равнодействующей силе, параллельной им, равной по величине их разности и направленной в сторону большей силы. Линия действия равнодействующей расположена за линией действия большей силы и делит отрезок прямой между линиями действия заданных сил на части, обратно пропорциональные силам.
2.3. Момент силы
Моментом силы называется физическая величина, характеризующая вращательный эффект действия силы.
2.3.1. Момент силы относительно центра
Момент силы 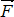 относительно центра О есть вектор
относительно центра О есть вектор .png) , приложенный в этом центре, который направлен перпендикулярно плоскости, проходящей через центр О и силу
, приложенный в этом центре, который направлен перпендикулярно плоскости, проходящей через центр О и силу 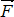 , в ту сторону, откуда сила видна стремящейся повернуть тело вокруг центра О против хода часовой стрелки (рис. 2.3а).
, в ту сторону, откуда сила видна стремящейся повернуть тело вокруг центра О против хода часовой стрелки (рис. 2.3а).
Момент силы 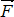 относительно центра О равен векторному произведению радиуса-вектора, проведенного из центра О в точку А, где приложена сила, на саму силу:
относительно центра О равен векторному произведению радиуса-вектора, проведенного из центра О в точку А, где приложена сила, на саму силу:
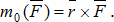
Момент силы 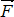 относительно центра О характеризуется:
относительно центра О характеризуется:
1) положением в пространстве плоскости ОАВ (плоскости поворота), проходящей через центр О и силу 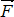 ;
;
2) направлением поворота;
3) модулем момента силы.
Модуль момента силы определяется по правилу умножения векторов: модуль векторного произведения двух векторов равен произведению модулей этих векторов на синус угла между ними:
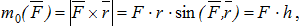
т.к. 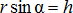 , где h – кратчайшее расстояние от точки О до линии действия силы
, где h – кратчайшее расстояние от точки О до линии действия силы  - называется плечом силы.
- называется плечом силы.
Алгебраическим моментом силы относительно точки называется скалярная величина, равная произведению модуля силы на плече силы относительно этой точки.
Плечом силы  относительно точки называется кратчайшее расстояние h от этой точки до линии действия силы.
относительно точки называется кратчайшее расстояние h от этой точки до линии действия силы.
Если сила стремится повернуть тело против хода часовой стрелки, то величина момента силы берётся со знаком «плюс», если по ходу часовой стрелки – знак «минус».
Свойства момента силы:
а) момент силы равен нулю, если сила равна нулю или когда плечо равно нулю, т.е. линия действия силы проходит через моментную точку,
б) величина момента силы относительно точки не изменяется при переносе силы вдоль линии её действия,
в) момент силы численно равен удвоенной площади треугольника, построенного на силе F и полюсе О (рис.2.3б).
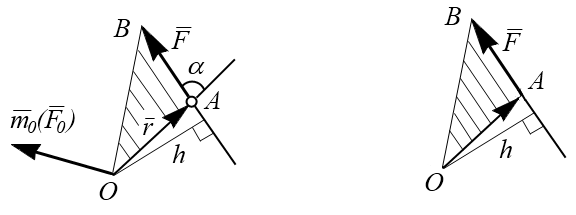
Рис.2.3
Таким образом, алгебраический моменты силы 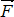 относительно точки О равен:
относительно точки О равен: 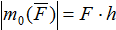 (Н∙м).
(Н∙м).
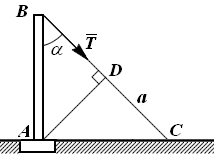
Рис. 2.4
Пример. Веревка ВС длиной а, привязанная к столбу под углом α, натягивается с силой, величина которой равна Т (рис. 2.4). Определить момент этой силы относительно точки А.
Решение.
Проведем перпендикуляр AD из точки А на линию действия силы 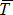 . Из треугольника АВD имеем:
. Из треугольника АВD имеем: 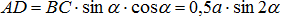 .
.
Так как сила 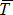 стремится вращать столб АВ вокруг точки А по ходу часовой стрелки, то момент силы
стремится вращать столб АВ вокруг точки А по ходу часовой стрелки, то момент силы 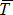 относительно точки А – отрицателен, т.е.
относительно точки А – отрицателен, т.е. 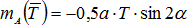 .
.
2.3.2. Пара сил. Момент пары
Система двух равных по величине, параллельных и противоположно направленных сил 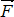 и
и 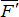 , приложенных к твердому телу, называется парой сил (рис. 2.5). Так как
, приложенных к твердому телу, называется парой сил (рис. 2.5). Так как 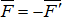 , то
, то 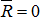 . Следовательно, пара сил не имеет равнодействующей. В то же время, эта система сил не является уравновешенной, поскольку силы
. Следовательно, пара сил не имеет равнодействующей. В то же время, эта система сил не является уравновешенной, поскольку силы 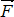 и
и 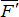 не направлены вдоль одной прямой. Расстояние между линиями действия сил называется плечом пары d. Момент пары сил равен произведению одной из сил пары на плечо. Знак момента пары определяется так же, как и момент силы относительно центра.
не направлены вдоль одной прямой. Расстояние между линиями действия сил называется плечом пары d. Момент пары сил равен произведению одной из сил пары на плечо. Знак момента пары определяется так же, как и момент силы относительно центра.
Рис. 2.5
Пару сил обычно прикладывают к твердому телу, чтобы сообщить ему вращение вокруг оси (рис. 2.6).
Рис. 2.6
Силы, входящие в состав пары сил, обладают всеми свойствами любых других сил, приложенных к твердому телу. Они являются скользящими векторами, их можно складывать с другими силами системы сил, добавлять к паре сил и отбрасывать системы сил, эквивалентные нулю. Действие пары сил на твердое тело зависит от плоскости действия пары сил, ее момента, определяющего вращательную способность и направление вращения, в котором пара сил стремиться вращать тело.
2.3.3. Теорема об алгебраической сумме момента сил пары относительно любой точки, лежащей в плоскости действия пары
Пусть на тело действует пара сил 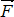 и
и 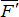 . Выберем произвольную точку О и определим момент сил пары относительно этой точки (рис.2.7).
. Выберем произвольную точку О и определим момент сил пары относительно этой точки (рис.2.7).
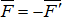
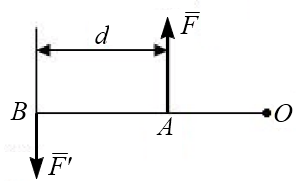
Рис. 2.7
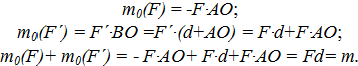
Алгебраическая сумма моментов сил пары, взятых относительно некоторой неподвижной точки, лежащей в плоскости действия пары, не зависит от выбора этой точки и равна моменту пары.
2.3.4. Теорема об эквивалентности пар
Рассмотрим пару сил 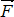 и
и 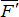 , действующую на твёрдое тело (рис.2.8).
, действующую на твёрдое тело (рис.2.8).
Проведём в плоскости действия пары через произвольные точки K и L две параллельные прямые до их пересечения с линиями действия сил 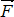 и
и 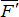 . Перенесём силы
. Перенесём силы 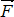 и
и 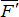 в точки пересечения прямых А и В. Разложим силы
в точки пересечения прямых А и В. Разложим силы 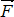 и
и 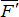 на составляющие по направлению AB и KB.
на составляющие по направлению AB и KB. 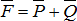 ,
, 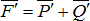 . Очевидно, что
. Очевидно, что 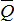 и
и 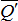 можно отбросить, как уравновешенную систему сил. В результате пара
можно отбросить, как уравновешенную систему сил. В результате пара 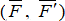 заменяется парой
заменяется парой 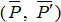 с плечом d2.
с плечом d2.
Покажем, что пары 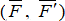 и
и 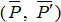 имеют одинаковые моменты:
имеют одинаковые моменты:
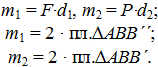
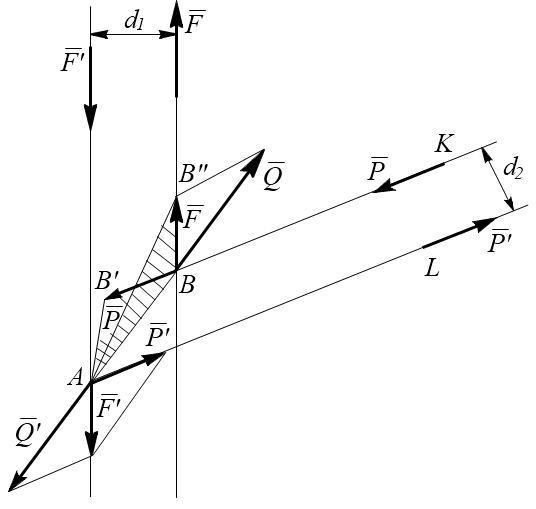
Рис. 2.8
Площади треугольников АВВ´´ и АВВ´ равны, так как у них общее основание АВ и одинаковая высота, т.к. АВ||В´В´´.
Следовательно: m1 = F•d1 = m2 = Р•d2.
Силы 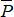 и
и  можно перенести вдоль линии их действия и приложить к точкам K и L. По теореме об эквивалентности пар: пару сил, действующую на твёрдое тело, можно заменить другой парой, расположенной в той же плоскости и имеющей тот же алгебраический момент.
можно перенести вдоль линии их действия и приложить к точкам K и L. По теореме об эквивалентности пар: пару сил, действующую на твёрдое тело, можно заменить другой парой, расположенной в той же плоскости и имеющей тот же алгебраический момент.
Из доказанной теоремы следует, что пару сил можно переносить в плоскости действия пары (рис. 2.9а и б) и у данной пары можно произвольно менять модуль силы и длину плеча, сохраняя неизменным её момент.

Рис. 2.9
На чертежах пару сил принято изображать изогнутым вектором с указанием величины момента.
2.3.5. Сложение пар, расположенных в одной плоскости
Система пар, расположенных в одной плоскости может быть заменена одной парой, расположенной в той же плоскости с моментом, равным алгебраической сумме моментов слагаемых пар.
Пусть на тело действует система пар m1, m2 , m3, расположенных в одной плоскости (рис. 2.10).
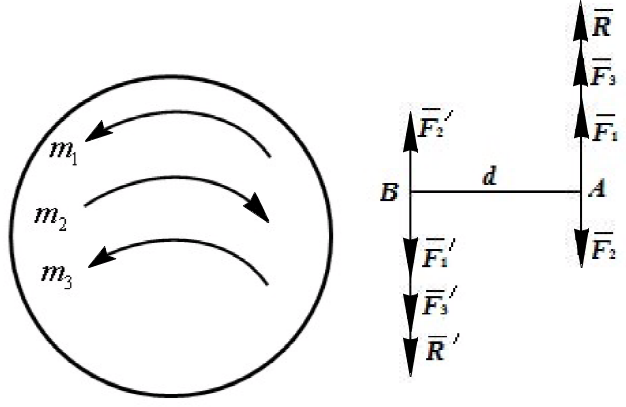
Рис. 2.10
Согласно теореме об эквивалентности пар, у любой пары можно произвольно менять силу и плечо пары, сохраняя неизменным его момент. Примем для всех пар одно и то же плечо d = AB (рис. 2.10). Следовательно, силы пар должны быть соответственно равны:
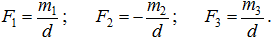
Приложим силы к точкам А и В. Сложив силы, получим их равнодействующие:
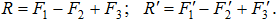
Силы 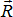 и
и 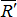 образуют новую пару, поскольку
образуют новую пару, поскольку 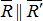 и
и 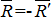 , с общим плечом d:
, с общим плечом d:
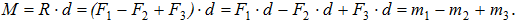
Если на тело действует n пар, лежащих в одной плоскости, то результирующая пара равна их алгебраической сумме:
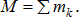
Из полученного результата вытекает условие равновесия пар: для равновесия пар, расположенных в одной плоскости, необходимо и достаточно, чтобы алгебраическая сумма моментов пар была равна нулю:
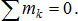
2.3.6. Теорема о моменте равнодействующей плоской системы сходящихся сил (теорема Вариньона)
Момент равнодействующей плоской системы сходящихся сил относительно любой точки, лежащей в плоскости действия сил, равен алгебраической сумме моментов слагаемых сил относительно этой точки (рис. 2.11).
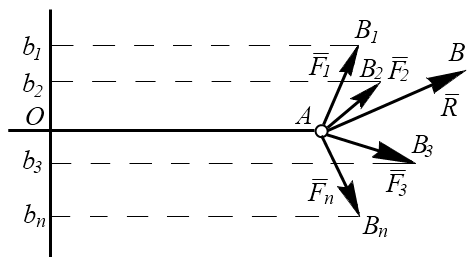
Рис. 2.11
Рассмотрим систему сил, сходящихся в точке А.
Выберем произвольную точку О и соединим ее с точкой А. Через точку О проведем ось Ох перпендикулярно ОА. Ось х направим так, чтобы проекция силы на эту ось и величина момента силы относительно точки О были одинакового знака. Спроецируем все силы на ось Ох: 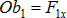 ,
, 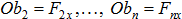 .
.
Момент силы 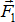 относительно точки О:
относительно точки О: 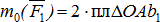 и т.д.
и т.д. 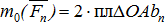 . Сложим сходящиеся силы. Равнодействующая сходящихся сил равна
. Сложим сходящиеся силы. Равнодействующая сходящихся сил равна 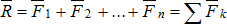 . Спроецируем векторное равенство на ось Ох:
. Спроецируем векторное равенство на ось Ох: 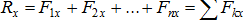 . Умножим левую и правую части полученного выражения на ОА, получим:
. Умножим левую и правую части полученного выражения на ОА, получим: 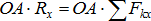 ,
, 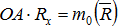 ,
, 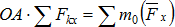 . Следовательно,
. Следовательно, 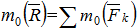 .
.
Теорема доказана.
Эта теорема позволяет определить момент силы относительно центра в том случае, если определение плеча силы вызывает затруднение.
Пример. Определить момент силы 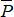 , приложенной к раме, относительно точки А (рис. 2.12). Разложим силу
, приложенной к раме, относительно точки А (рис. 2.12). Разложим силу 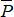 на составляющие
на составляющие 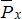 и
и 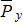 и определим их моменты относительно выбранной точки.
и определим их моменты относительно выбранной точки.
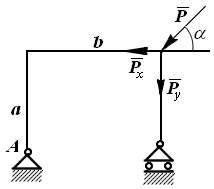
Рис. 2.12
Согласно теореме Вариньона:
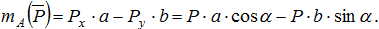
2.4. Теорема о параллельном переносе силы (метод Пуансо)
Пусть на тело действует сила 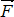 , приложенная в точке А (рис.2.13).
, приложенная в точке А (рис.2.13).
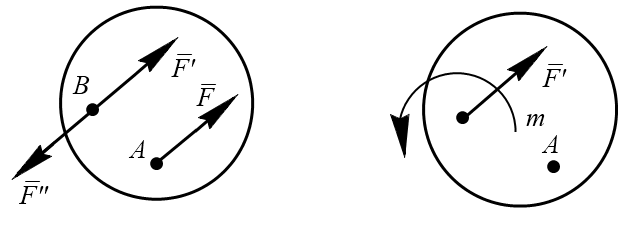
Рис. 2.13
Действие этой силы не изменится (согласно второй аксиомы статики), если в произвольной точке В тела приложить две уравновешенные силы 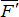 и
и 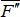 , такие, что
, такие, что 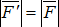 ,
, 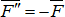 . Полученная система трех сил и представляет собой силу
. Полученная система трех сил и представляет собой силу 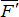 равную
равную 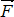 , но приложенную в точке В, и пару
, но приложенную в точке В, и пару 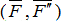 , момент которой равен
, момент которой равен 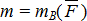 .
.
Следовательно, силу, приложенную к абсолютно твёрдому телу, можно не изменяя оказываемого ею действия, переносить параллельно ей самой из данной точки в любую другую точку тела, прибавляя при этом пару с моментом, равным моменту переносимой силы относительно точки, куда эта сила переносится. Тогда 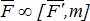 , где
, где 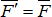 ,
, 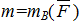 .
.
Пример. Чтобы удержать в равновесии однородный брус АВ длиной 2а и весом 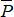 , надо приложить в его середине С направленную вверх силу
, надо приложить в его середине С направленную вверх силу 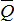 , по модулю равную
, по модулю равную 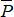 (рис. 2.14).
(рис. 2.14).
Рис. 2.14
Согласно доказанной теореме силу  можно заменить силой
можно заменить силой  , приложенной к концу А бруса и парой с моментом, модуль которого
, приложенной к концу А бруса и парой с моментом, модуль которого 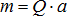 . Если плечо этой пары уменьшить до величины h, то образующие ее силы
. Если плечо этой пары уменьшить до величины h, то образующие ее силы 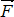 и
и 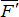 надо увеличить так, чтобы
надо увеличить так, чтобы 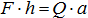 . Следовательно, чтобы удержать брус за конец А, надо, кроме силы
. Следовательно, чтобы удержать брус за конец А, надо, кроме силы 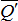 , приложить еще пару
, приложить еще пару 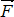 ,
, 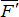 . Этот результат, вытекающий из теоремы «ощущает» рука человека, удерживающего брус за середину или за конец.
. Этот результат, вытекающий из теоремы «ощущает» рука человека, удерживающего брус за середину или за конец.
2.5. Приведение произвольной плоской системы сил к данному центру
Если на тело действует система сил, то, пользуясь методом Пуансо, все силы можно параллельно перевести в некоторый центр О и сложить их (рис. 2.15). Геометрическая сумма действующих на тело сил называется главным вектором 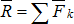 . Присоединённые пары сил также можно сложить.
. Присоединённые пары сил также можно сложить.
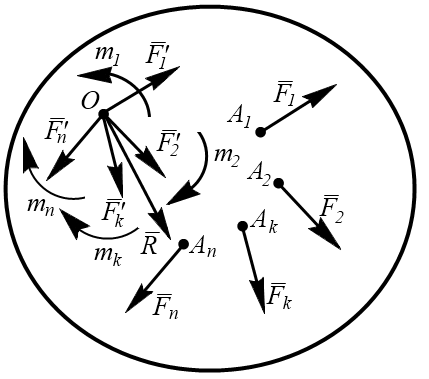
Рис. 2.15
Алгебраическая сумма сил пары называется главным моментом системы относительно центра приведения 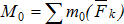 .
.
Следовательно, плоская система сил, действующих на абсолютно твердое тело, при приведении к произвольно выбранному центру О заменяется одной силой 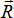 , равной главному вектору системы сил и приложенной в центре приведения О, и одной парой с моментом
, равной главному вектору системы сил и приложенной в центре приведения О, и одной парой с моментом 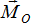 , равным главному моменту системы сил относительно центра О, но сила и пара лежат в данном случае в одной плоскости – в плоскости действия сил.
, равным главному моменту системы сил относительно центра О, но сила и пара лежат в данном случае в одной плоскости – в плоскости действия сил.
2.6. Приведение плоской системы сил к простейшему виду
Частные случаи приведения плоской системы сил приведены в табл. 2.1.
Таблица 2.1
Частные случаи приведения плоской системы сил к простейшему виду
|
№
|
Значения главного вектора и главного момента
|
Результат приведения
|
|
1
|
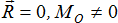
|
Система сил приводится к паре сил, момент которой равен главному моменту MO (главный момент системы сил не зависит от выбора центра приведения О).
|
|
2
|
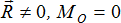
|
Система сил приводится к равнодействующей, равной 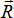 , проходящей через центр О. , проходящей через центр О.
|
|
3
|
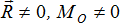
|
Система сил приводится к равнодействующей, равной 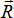 , линия действия которой отстоит от линии действия силы , линия действия которой отстоит от линии действия силы 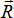 на расстояние на расстояние 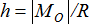 . Положение линии действия равнодействующей должно быть таким, чтобы знак момента равнодействующей относительно центра приведения О совпадал со знаком главного момента системы сил MO относительно центра О. Сила . Положение линии действия равнодействующей должно быть таким, чтобы знак момента равнодействующей относительно центра приведения О совпадал со знаком главного момента системы сил MO относительно центра О. Сила 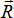 и равнодействующая равны по модулю и параллельны. и равнодействующая равны по модулю и параллельны.
|
|
4
|
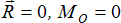
|
Система сил, приложенных к твердому телу, является уравновешивающейся.
|
2.7. Формы уравнений равновесия произвольной плоской системы сил
Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы выполнялось одно из следующих условий равновесия (табл. 2.2).
Таблица 2.2
Формы уравнений равновесия произвольной системы сил
|
№
|
Условие
|
Комментарии
|
|
1
|
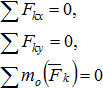
- основная форма условий равновесия.
|
Сумма проекций всех сил на произвольно выбранные оси декартовых координат x и y и сумма моментов этих сил относительно любого центра О, лежащего в плоскости действия сил, равнялись нулю.
|
|
2
|
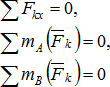
- уравнения проекций и двух уравнений моментов относительно двух точек. 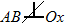
|
Суммы моментов всех сил относительно двух центров А и В и сумма проекций всех сил на ось Ох, не перпендикулярную прямой АВ, были равны нулю.
|
|
3
|
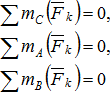
- уравнения моментов относительно трех выбранных точек.
|
Суммы моментов всех сил относительно любых трех центров А, В, С, не лежащих на одной прямой, были равны нулю.
|
Равновесие плоской системы параллельных сил. В том случае, когда все силы параллельны друг другу, одну из координатных осей следует направить параллельно силам.
Для параллельных сил (параллельны оси Оу) останется два условия равновесия (табл. 2.3).
Таблица 2.3
Условия равновесия плоской системы параллельных сил
|
№
|
Условие
|
Комментарии
|
|
1
|
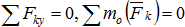
(ось Oy параллельна силам)
|
Сумма проекций всех сил на ось декартовых координат y и сумма моментов этих сил относительно любого центра О, лежащего в плоскости действия сил, равнялись нулю.
|
|
2
|
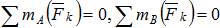
АВ не должна быть параллельна силам 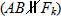
|
Суммы моментов всех сил относительно двух центров А и В были равны нулю.
|
2.8. Методические указания к решению задач по исследованию условий равновесия произвольной плоской системы сил, приложенной к твердому телу
При практическом решении задач можно пользоваться любой формой уравнений равновесия, так как все они совершенно равноправны. Изложим некоторые общие правила составления уравнения равновесия.
Оси координат и моментные точки можно выбирать произвольно. Наиболее просто и безошибочно решаются уравнения равновесия, в которые входит одно неизвестное. Следовательно, координатные оси надо направлять перпендикулярно к направлению неизвестных сил. Тогда при составлении уравнений проекций неизвестные, перпендикулярные к осям, в эти уравнения не войдут. За моментные целесообразно брать такие точки, в которых пересекаются линии действия двух неизвестных сил. Тогда в уравнение моментов войдет только одна искомая сила.
Для плоской системы можно выбирать любое число координатных осей и моментных точек и составлять соответствующее число уравнений равновесия, но только три из них будут независимыми. Остальные уравнения получаются как следствия из этих трех и их можно использовать лишь для проверки.
Для плоской системы параллельных сил эти общие правила можно конкретизировать. Оси координат следует направлять так, чтобы одна из них оказалась параллельной силам, приложенным к твердому телу. Уравнение моментов нужно составлять относительно точки, лежащей на линии действия неизвестной силы. Это дает возможность определить одну из неизвестных сил непосредственно из одного уравнения моментов. Для решения задач при помощи двух уравнений моментов следует учитывать, что моментные точки не должны лежать на прямой, параллельной силам.
Задачи на равновесие твердого тела для плоской системы сил рекомендуется решать в следующем порядке:
1. Выделить тело, равновесие которого надо рассмотреть.
2. Изобразить активные (заданные) силы.
Освободить тело от связей, приложив соответствующие реакции. При этом необходимо убедиться, что данная задача является статически определимой – число неизвестных величин должно быть не более трех (для системы параллельных сил – не более двух).
3. Направить оси координат и выбрать моментные точки.
4. Составить уравнения равновесия произвольной плоской системы сил (или плоской системы параллельных сил).
5. Решить систему полученных уравнений равновесия относительно неизвестных величин.
Если в результате решения искомая реакция получается положительной, то это значит, что направление ее выбрано верно, если отрицательной, то направление реакции противоположно выбранному (модуль ее при этом остается прежним).
После того как задача решена, необходимо произвести проверку. Для этого следует составить не применявшуюся при решении сумму моментов или проекций, при этом необходимо учитывать уже исправленные направления реакций. Равенство нулю алгебраической суммы проекций или моментов подтвердит правильность решения задачи.
Пример решения задачи с использованием первой (основной) формы уравнений равновесия
Пример. Горизонтальная балка длиной 5 м заделана в стену (рис.2.16). На балку действует равномерно распределенная нагрузка интенсивностью q=1,5 Н/м на участке длиной 3 м, а также пара сил с моментом 2 Н•м и сила F = 4Н.
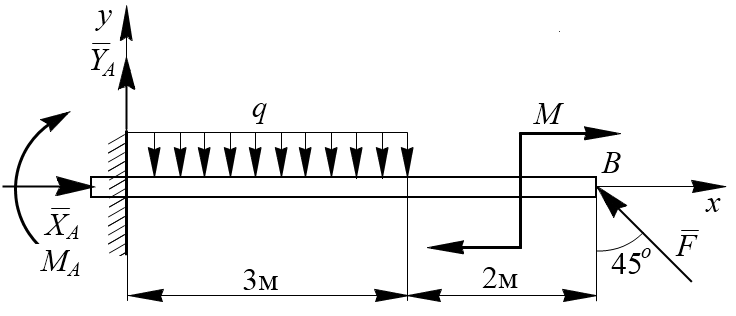
Рис. 2.16
Определить реакции заделки (XA, YA, MA).
Решение: Задача сводится к определению реакции опоры жесткой заделки, при действии на балку равномерно распределенной нагрузки, момента пары сил и силы, приложенной к концу балки под углом 45°.
1. Рассматриваем равновесие плоской системы сил, действующей на балку.
2. Показываем все действующие на балку силы и момент пары сил.
3. Мысленно отбрасываем связи и заменяем их реакциями XA, YA, MA. Направления XA, YA принимаем совпадающими с направлением осей координат Axy.
4. Составляем три уравнения равновесия:
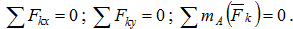
Из трех уравнений можно определить три неизвестные величины.
Составим уравнение равновесия сил:
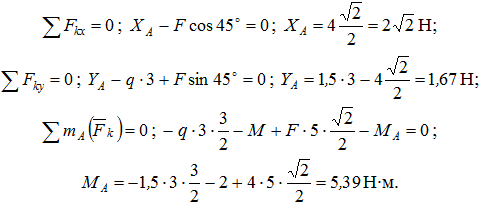
Проверка. Сумма моментов относительно точки В:
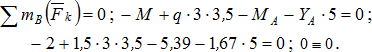
Проверка сошлась.
Пример решения задачи с использованием второй формы уравнений равновесия
Пример. Однородная балка АВ весом 20 кг опирается на гладкий горизонтальный пол в точке В под углом 60° и, кроме того, поддерживается двумя опорами С и D (рис. 2.17).
Определить реакции опор в точках В, С и D, если длина АВ = 3 м, СВ= 0,5 м, BD = 1 м.
Дано: Р = 200Н; АВ = 3м; СВ = 0,5м; ВD = 1м.
Найти: NC, ND, NB - ?
Решение: Задача сводится к определению реакций опор в точках В, С, D при действии на балку силы тяжести Р = 200Н.
1. Рассмотрим равновесие плоской системы сил, действующей на балку.
2. Приложим посередине балки силу тяжести 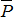 .
.
3. Проведем оси координат через точку B, направив ось x параллельно оси балки.
4. Мысленно отбрасываем связи и заменяем их реакциями 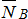 ,
, 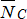 ,
, 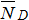 .
.
5. Составляем три уравнения равновесия: 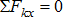 ;
; 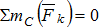 ;
; 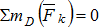 , из которых можно найти три неизвестных величины.
, из которых можно найти три неизвестных величины.
Составим уравнения равновесия сил:
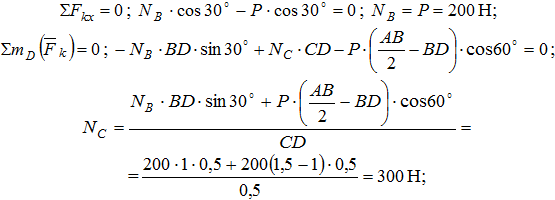
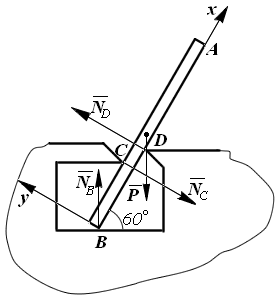
Рис. 2.17
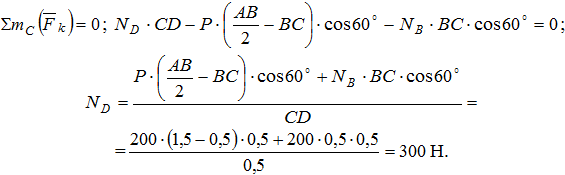
Проверка. Сумма моментов относительно точки В:
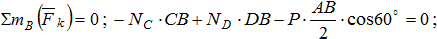
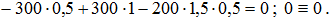
Проверка сошлась.
Пример решения задачи с использованием третьей формы уравнений равновесия
Пример. Тяжелая балка силой тяжести G удерживается в горизонтальном положении на трех тросах (рис. 2.18). Определить натяжения тросов.
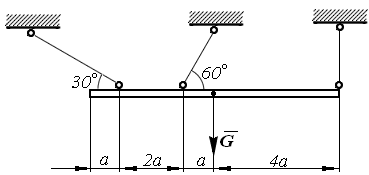
Рис. 2.18
Решение. Рассмотрим равновесие балки. К ней приложена активная сила 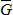 . Отбросим связи, заменив их реакциями тросов:
. Отбросим связи, заменив их реакциями тросов: 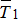 ,
, 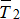 и
и 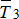 , численно равными искомым натяжениям. Задача статически определима, так как имеется три неизвестных. Выберем три моментные точки А, В и С (рис. 2.19), в каждой из которых пересекаются по две неизвестные силы, и составим три уравнения:
, численно равными искомым натяжениям. Задача статически определима, так как имеется три неизвестных. Выберем три моментные точки А, В и С (рис. 2.19), в каждой из которых пересекаются по две неизвестные силы, и составим три уравнения:
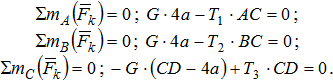
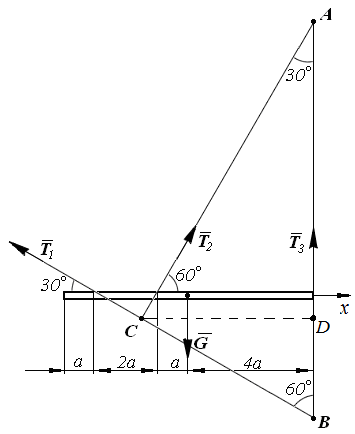
Рис. 2.19
Находим величины АС, ВС и СD:
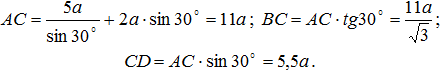
Тогда, решая полученную систему уравнений, получим, что:
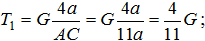
Проверка. Сумма проекций всех сил на ось Ox:
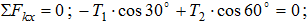
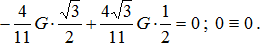
Проверка сошлась.