1.1. Основные понятия статики
Статикой называется раздел теоретической механики, в котором излагается общее учение о силах и изучаются условия равновесия тел, находящихся под действием сил.
Силой называется физическая величина, являющаяся мерой механического взаимодействия тел. Сила – величина векторная. Она характеризуется величиной (модулем), направлением и точкой приложения. Основной единицей измерения силы является Ньютон [Н].
В статике все тела считаются абсолютно твёрдыми, то есть под действием сил их форма и размеры остаются неизменными.
Совокупность сил, приложенных к телу, называется системой сил. Если все силы лежат в одной плоскости, то такая система сил называется плоской. Если силы не лежат в одной плоскости, то они образуют пространственную систему сил.
Тело, которое из данного положения может переместиться в любое положение в пространстве, называется свободным телом.
Две системы сил называют эквивалентными одна другой, если каждая из них, действуя по отдельности, может сообщить покоящемуся телу одно и то же движение 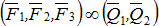 .
.
Система сил, под действием которой покоящееся тело не изменяет своего состояния покоя, называется уравновешенной или эквивалентной нулю – 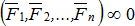 .
.
Сила, которая одна заменяет действие системы сил на твёрдое тело, называется равнодействующей – 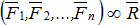 .
.
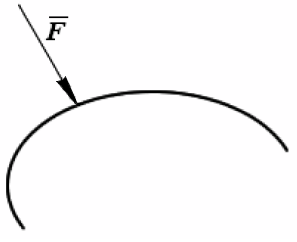
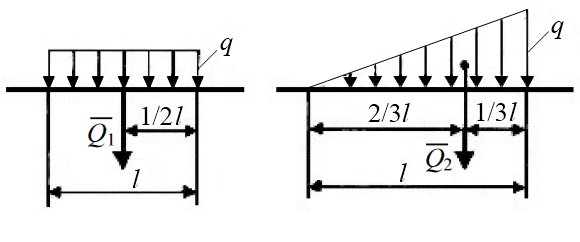
Силы могут быть сосредоточенные (рис. 1.1, а) и распределенные (рис. 1.1, б). Сила, приложенная к какой-нибудь одной точке тела, называется сосредоточенной.
Система распределенных сил характеризуется интенсивностью q, т.е. значением силы, приходящейся на единицу длины нагруженного отрезка. Измеряется интенсивность в Ньютонах, деленных на метры (Н/м).
|
|
|
а
|
б
|
Рис. 1.1
Распределенную нагрузку в виде прямоугольника (равномерно распределенная нагрузка) или треугольника заменяют одной силой (равнодействующей), которую прикладывают в центре тяжести площади распределения (рис. 1.1, б). Величина равнодействующей численно равна площади фигуры, образованной распределенной нагрузкой: 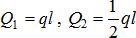 .
.
1.2. Аксиомы статики
В основе статики лежат некоторые основные положения (аксиомы), которые являются обобщением многовекового производственного опыта человечества и теоретических исследований.
Аксиома 1. Если на свободное абсолютно твёрдое тело действуют две силы, то тело может находиться в равновесии тогда и только тогда, когда эти силы равны по величине и направлены вдоль одной прямой в противоположные стороны (рис.1.2).

Рис.1.2
Аксиома 2. Действие данной системы сил на абсолютно твёрдое тело не изменится, если к ней прибавить или от неё отнять уравновешенную систему сил. Если  , то
, то 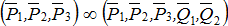 .
.
Следствие: действие силы на абсолютно твёрдое тело не изменится, если перенести точку приложения силы вдоль её линии действия в любую другую точку тела.
Пусть на тело действует приложенная в точке А сила  . Выберем на линии действия этой силы произвольную точку В, и приложим к ней уравновешенные силы
. Выберем на линии действия этой силы произвольную точку В, и приложим к ней уравновешенные силы  и
и  , причём
, причём 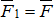 ,
, 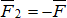 . Так как силы
. Так как силы 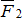 и
и 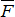 образуют уравновешенную систему сил, то согласно второй аксиоме статики их можно отбросить. В результате на тело будет действовать только одна сила
образуют уравновешенную систему сил, то согласно второй аксиоме статики их можно отбросить. В результате на тело будет действовать только одна сила 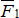 , равная
, равная 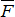 , но приложенная в точке В (рис.1.3).
, но приложенная в точке В (рис.1.3).
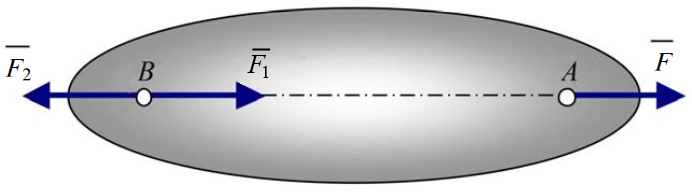
Рис.1.3
Аксиома 3. Две силы, приложенные к твёрдому телу в одной точке, имеют равнодействующую, приложенную в той же точке и изображаемую диагональю параллелограмма, построенного на этих силах как на сторонах.
Вектор 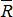 , равный диагонали параллелограмма, построенного на векторах
, равный диагонали параллелограмма, построенного на векторах 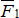 и
и 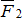 , называется геометрической суммой векторов
, называется геометрической суммой векторов 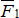 и
и 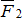 (рис.1.4).
(рис.1.4).
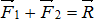
Рис.1.4
Аксиома 4. Закон равенства действия и противодействия.
При всяком действии одного тела на другое имеет место такое же по величине, но противоположное по направлению противодействие (рис.1.5).
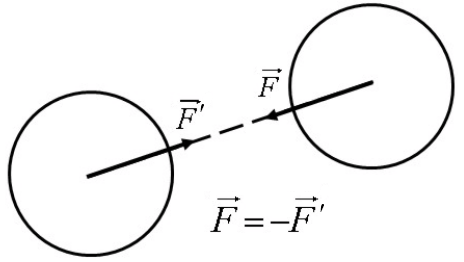
Рис.1.5
Аксиома 5. Принцип отвердевания.
Равновесие изменяемого (деформируемого) тела, находящегося под действи-ем данной системы сил, не нарушится, если тело считать отвердевшим, т.е. абсолютно твёрдым.
1.3. Виды связей и их реакции
Связями называются любые ограничения, препятствующие перемещению тела в пространстве.
Тело, стремясь под действием приложенных сил осуществить переме-щение, которому препятствует связь, будет действовать на нее с некоторой силой, называемой силой давления на связь. По закону о равенстве действия и противодействия, связь будет действовать на тело с такой же по модулю, но противоположно направленной силой.
Сила, с которой данная связь действует на тело, препятствуя тем или иным перемещениям, называется силой реакции (реакцией) связи.
Одним из основных положений механики является принцип освобождаемости от связей: всякое несвободное тело можно рассматривать как свободное, если отбросить связи и заменить их действие реакциями связей. Реакция связи направлена в сторону, противоположную той, куда связь не дает перемещаться телу. Основные виды связей и их реакции приведены в таблице 1.1.
Таблица 1.1
Виды связей и их реакции
|
№
|
Наименование связи
|
Условное обозначение
|
|
1
|
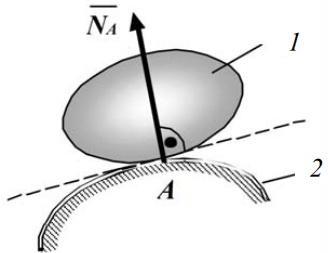
Гладкая поверхность (опора) – поверхность (опора), трением о которую данного тела можно пренебречь.
При свободном опирании реакция 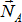 направляется перпендикулярно касательной, проведенной через точку А контакта тела 1 с опорной поверхностью 2. направляется перпендикулярно касательной, проведенной через точку А контакта тела 1 с опорной поверхностью 2.
|
|
|
2
|
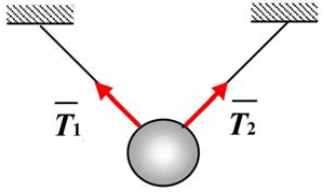
Нить (гибкая, нерастяжимая). Связь, осуществлённая в виде нерастяжимой нити, не позволяет телу удаляться от точки подвеса. Поэтому реакция нити направлена вдоль нити к точке её подвеса.
|
|
|
3
|
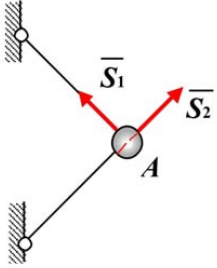
Невесомый стержень – стержень, весом которого по сравнению с воспринимаемой нагрузкой можно пренебречь.
Реакция невесомого шарнирно прикрепленного прямолинейного стержня направлена вдоль оси стержня.
|
|
|
4
|
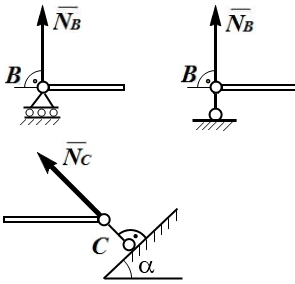
Подвижный шарнир, шарнирно-подвижная опора. Реакция направлена по нормали к опорной поверхности.
|
|
|
5
|
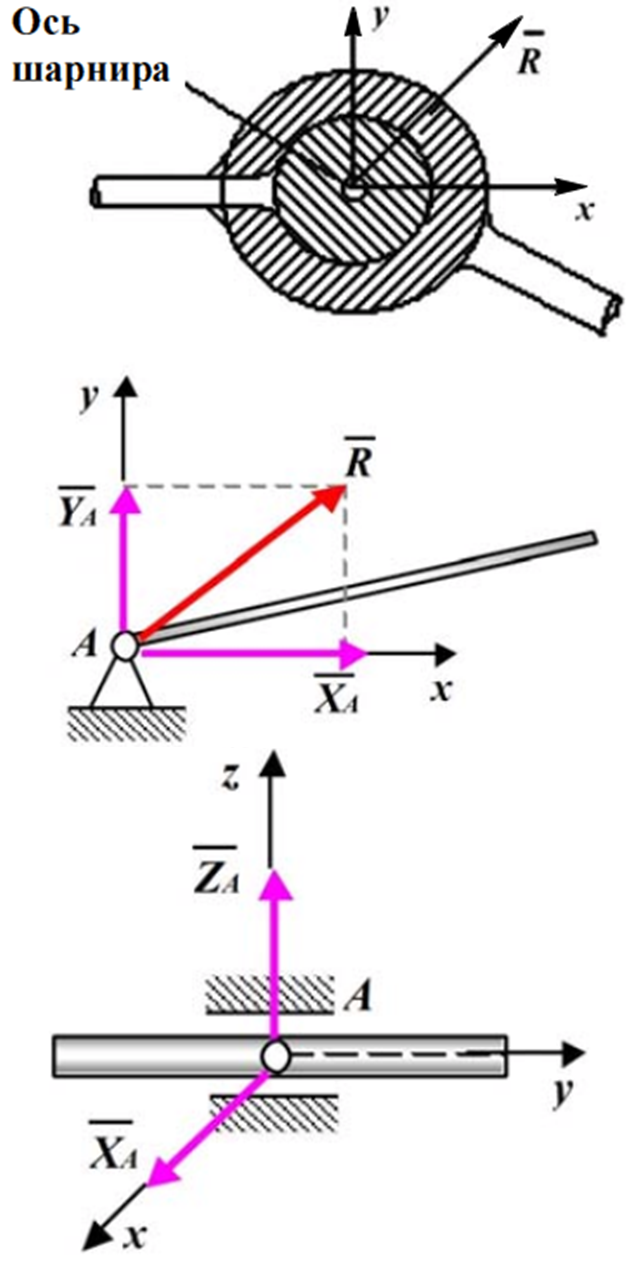
Цилиндрический шарнир (подшипник, шарнирно-неподвижная опора). При осуществлении связи в виде цилиндрического шарнира одно тело может поворачиваться относительно другого вокруг общей оси, называемой осью шарнира.
Реакция 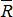 цилиндрического шарнира заранее не известна ни по величине, ни по на-правлению; может иметь любое направление в плоскости, перпендикулярной оси шарнира. цилиндрического шарнира заранее не известна ни по величине, ни по на-правлению; может иметь любое направление в плоскости, перпендикулярной оси шарнира.
Модуль и направление полной реакции определяют две составляющие реакции в этой плоскости.
|
|
|
6
|
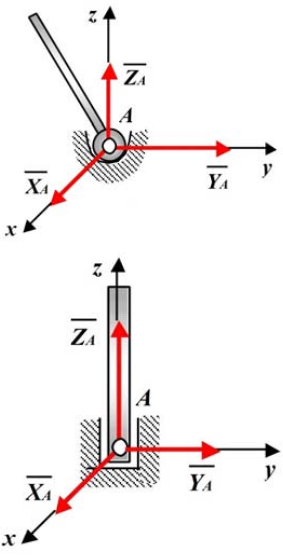
Сферический (шаровый) шарнир, подпятник. Тела, соединённые с помощью сферического шарнира, могут как угодно поворачиваться относительно центра шарнира. Реакция сферического шарнира 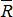 может иметь любое направление в пространстве. может иметь любое направление в пространстве.
Реакция сферического шарнира и подпятника (подшипника с упором) может иметь любое направление в пространстве. Три составляющие 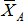 , ,  , ,  реакции определяют модуль и направление полной реакции. реакции определяют модуль и направление полной реакции.
|
|
|
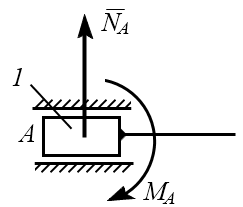
7
|
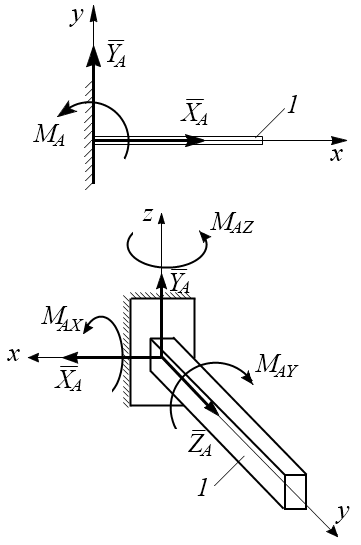
Жесткая заделка. В плоскости жесткой заделки будут две составляющие реакции 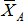 , , 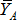 и момент пары сил и момент пары сил 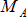 , который препятствует повороту балки 1 относительно точки А. , который препятствует повороту балки 1 относительно точки А.
Жесткая заделка в пространстве отнимает у тела 1 все шесть степеней свободы – три переме-щения вдоль осей координат и три поворота отно-сительно этих осей.
В пространственной жесткой заделке будут три составляющие 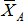 , , 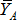 , , 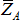 и три момента пар сил и три момента пар сил  . .
|
|
|
8
|
Ползун 1 на стержне 2. Рекция  направлена перпендикулярно стержню 2, момент пары сил направлена перпендикулярно стержню 2, момент пары сил 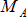 препятствует повороту ползуна 1 относительно точки А. препятствует повороту ползуна 1 относительно точки А.
|
|
|
9
|
Ползун 1 в направляющих. Рекция  направлена перпендикулярно направляющим, момент пары сил направлена перпендикулярно направляющим, момент пары сил  препятствует повороту ползуна 1 относительно точки А. препятствует повороту ползуна 1 относительно точки А.
|
|
1.4. Система сходящихся сил
1.4.1. Геометрический способ сложения сходящихся сил
Системой сходящихся сил называется система сил, линии действия которых пересекаются в одной точке. Две силы, сходящиеся в одной точке, согласно третьей аксиоме статики можно заменить одной силой – равнодействующей.
Решение многих задач статики связано с операцией сложения векторов, в частности, сил.
Главный вектор системы сил – величина, равная геометрической сумме сил системы. Главный вектор системы сил не следует путать с равнодействующей. Равнодействующая – всегда главный вектор, а главный вектор равен равнодействующей, если система сил является сходящейся.
Равнодействующую плоской системы сходящихся сил можно определить графически и графоаналитически.
Сложение двух сил. При графическом определении равнодействующей на чертеже и выбранном масштабе изображаются силы, затем они складываются по правилу параллелограмма. По длине диагонали параллелограмма, учитывая выбранный масштаб, определяется равнодействующая, равная сумме слагаемых сил. Точность определения равнодействующей зависит в этом случае от точности построения силового треугольника.
Графоаналитический способ сложения сил позволяет более точно определить равнодействующую, используя тригонометрические зависимости:
- теорему косинусов:
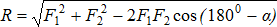
или 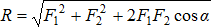 (рис.1.6);
(рис.1.6);
- теорему синусов:
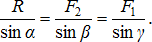
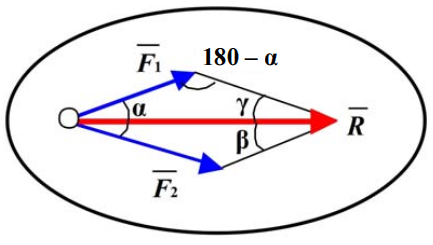
Рис. 1.6
Сложение трех сил, не лежащих в одной плоскости: геометрическую сумму  трех сил
трех сил  ,
,  ,
, 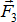 не лежащих в одной плоскости, изображают диагональю параллелепипеда (рис. 1.7), построенного на этих силах (правило параллелепипеда).
не лежащих в одной плоскости, изображают диагональю параллелепипеда (рис. 1.7), построенного на этих силах (правило параллелепипеда).
Рис. 1.7
Сложение системы сил. Сложение плоской системы сходящихся сил осуществляется либо путём последовательного сложения сил с построением промежуточной равнодействующей (рис. 1.8), либо путём построения силового многоугольника (рис. 1.9).
Рис. 1.8
Рис. 1.9
1.4.2. Разложение сил
Разложить данную силу на составляющие – означает найти такую систему сил, для которой данная сила является равнодействующей. Подобная задача имеет однозначное решение, если необходимо разложить силу по двум направлениям, лежащим в одной плоскости. На рис. 1.10 показано разложение силы F по двум направлениям ab и cd.
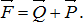
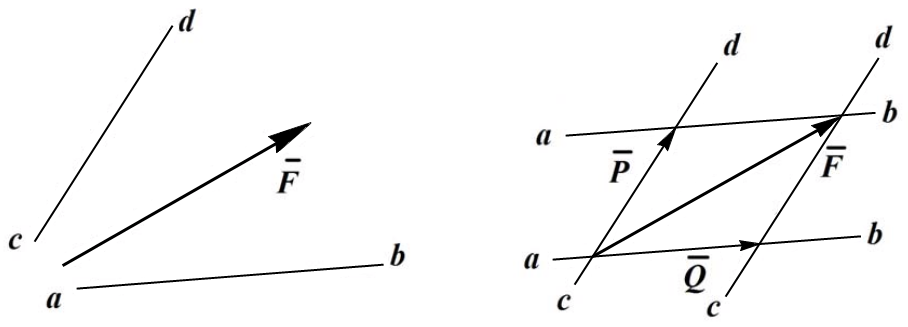
Рис. 1.10
1.4.3. Проекция силы на ось и на плоскость
Проекция силы на ось – алгебраическая величина, равная произведению модуля силы на косинус угла между силой и положительным направлением оси.
Проекция Fx (рис 1.11) силы  на ось х положительна, если угол α острый, отрицательна - если угол α тупой. Если сила
на ось х положительна, если угол α острый, отрицательна - если угол α тупой. Если сила  перпендикулярна оси, то ее проекция на ось равна нулю.
перпендикулярна оси, то ее проекция на ось равна нулю.
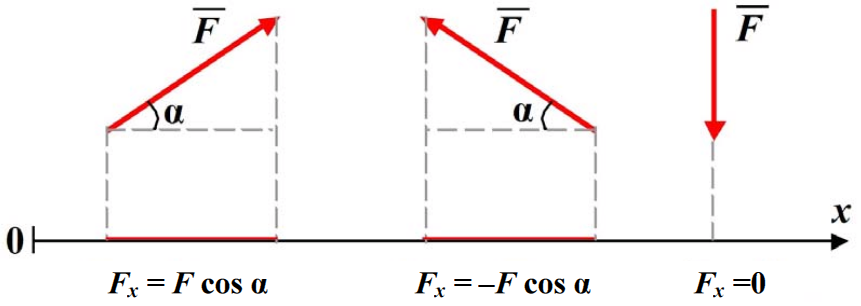
Рис. 1.11
Проекция силы 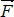 на плоскость Оху – вектор
на плоскость Оху – вектор 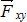 , заключенный между проекциями начала и конца силы
, заключенный между проекциями начала и конца силы  на эту плоскость. Т.е. проекция силы на плоскость величина векторная, характеризуется не только числовым значением, но и направлением в плоскости Оху (рис.1.12).
на эту плоскость. Т.е. проекция силы на плоскость величина векторная, характеризуется не только числовым значением, но и направлением в плоскости Оху (рис.1.12).
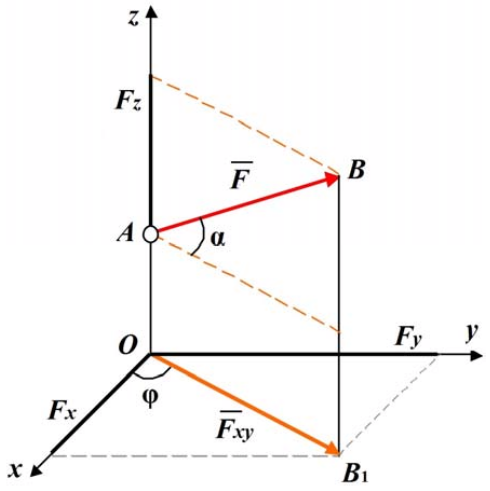
Рис. 1.12
Тогда модуль проекции 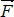 на плоскость Оху будет равен:
на плоскость Оху будет равен:
Fxy = F cosα,
где α - угол между направлением силы 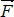 и ее проекцией
и ее проекцией 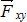 .
.
Если сила и ось координат не лежат в одной плоскости, то проекция силы на ось проводится методом двойного проецирования.
Например, чтобы определить проекцию силы 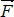 на ось х, надо спроецировать ее на плоскость Оху, а затем разложить проекцию силы
на ось х, надо спроецировать ее на плоскость Оху, а затем разложить проекцию силы 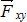 на составляющие по осям координат Fx и Fy (рис. 1.12).
на составляющие по осям координат Fx и Fy (рис. 1.12).
Fx = Fxy cosφ = F cosα cosφ;
Fy = Fxy sinφ = F cosα sinφ;
Fz = F sinα.
1.4.4. Аналитический способ задания и сложения сил
Аналитический способ задания сил. Для аналитического способа задания силы 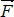 необходимо выбрать систему координатных осей Охуz, по отношению к которой будет определяться направление силы в пространстве.
необходимо выбрать систему координатных осей Охуz, по отношению к которой будет определяться направление силы в пространстве.
Вектор, изображающий силу 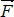 , можно построить, если известны модуль этой силы и углы α, β, γ, которые сила образует с координатными осями. Точка А приложения силы
, можно построить, если известны модуль этой силы и углы α, β, γ, которые сила образует с координатными осями. Точка А приложения силы 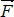 задается отдельно своими координатами х, у, z. Можно задавать силу ее проекциями Fx, Fy, Fz на координатные оси. Модуль силы в этом случае определится по формуле:
задается отдельно своими координатами х, у, z. Можно задавать силу ее проекциями Fx, Fy, Fz на координатные оси. Модуль силы в этом случае определится по формуле: 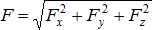 , а направляющие косинусы:
, а направляющие косинусы: 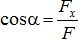 ,
, 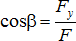 ,
, 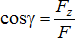 .
.
Аналитический способ сложения сил: проекция вектора суммы на какую–нибудь ось равна алгебраической сумме проекций слагаемых векторов на ту же ось, т.е., если: 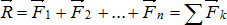 , то
, то 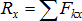 ,
, 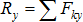 ,
,  .
.
Зная Rx, Ry, Rz, можем определить модуль 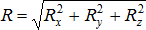 и направляющие косинусы:
и направляющие косинусы: 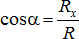 ,
, 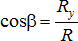 ,
, 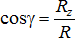 .
.
1.4.5. Условия равновесия плоской системы сходящихся сил
Для равновесия системы сходящихся сил необходимо и достаточно, чтобы равнодействующая этих сил была равна нулю.
1) Геометрическое условие равновесия сходящейся системы сил: для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный из этих сил, был замкнут (конец вектора последней слагаемой силы должен совместиться с началом вектора первой слагаемой силы). Тогда главный вектор системы сил будет равен нулю (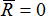 ).
).
2) Аналитические условия равновесия. Модуль главного вектора системы сил определяется по формуле 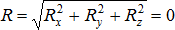 . Поскольку
. Поскольку 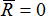 , то подкоренное выражение может быть равно нулю только в том случае, если каждое слагаемое одновременно обращается в нуль, т.е.
, то подкоренное выражение может быть равно нулю только в том случае, если каждое слагаемое одновременно обращается в нуль, т.е.
Rx = 0, Ry = 0, Rz = 0.
Следовательно, для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из трёх координат осей были равны нулю:
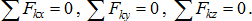
Для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы суммы проекций сил на каждую из двух координатных осей были равны нулю:
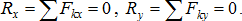
Теорема о трех силах: если твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости (рис. 1.13), то линии их действия пересекаются в одной точке (необходимое условие равновесия твердого тела).
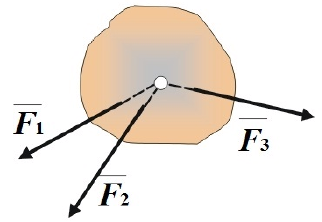
Рис. 1.13
Это условие равновесия не является достаточным, т.к. равнодействующая этих сил может оказаться не равной нулю.
Достаточным условием является наличие замкнутого силового треугольника при одновременном пересечения линий действия трех сил в одной точке.
Рассмотрим тело, на которое действуют три непараллельные силы  ,
,  и
и  (рис. 1.14).
(рис. 1.14).
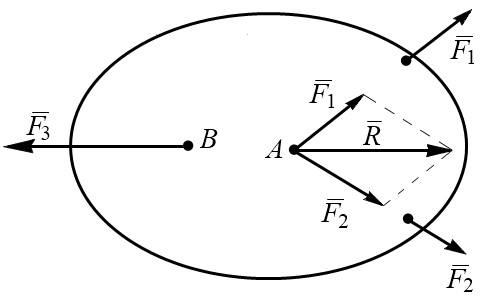
Рис. 1.14
Так как эти силы непараллельны, то две любые силы, например,  и
и  должны пересечься в некоторой точке А. Перенесём силы
должны пересечься в некоторой точке А. Перенесём силы 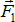 и
и 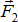 вдоль линии их действия и приложим их к точке А. Заменим сходящиеся силы
вдоль линии их действия и приложим их к точке А. Заменим сходящиеся силы 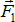 и
и 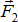 их равнодействующей
их равнодействующей 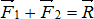 .
.
Следовательно, теперь на тело действуют только две силы 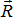 и
и 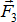 . Поскольку тело находится в равновесии под действием двух сил, то согласно первой аксиоме статики, эти силы должны действовать вдоль одной прямой АВ. Таким образом, линия действия силы
. Поскольку тело находится в равновесии под действием двух сил, то согласно первой аксиоме статики, эти силы должны действовать вдоль одной прямой АВ. Таким образом, линия действия силы 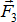 должна проходить через точку А.
должна проходить через точку А.
1.4.6. Методические указания к решению задач по исследованию условий равновесия системы сходящихся сил
Задачи данного типа могут решаться либо геометрическим (графическим) способом, либо аналитическим. При решении задач геометрическим (графическим) способом необходимо придерживаться следующего порядка:
1. Выделить тело (или точку), равновесие которого следует рассмотреть.
2. Изобразить все активные (заданные) силы, действующие на выделенное тело.
3. Освободить это тело от наложенных на него связей, заменив их действие реакциями связей.
4. Построить замкнутый силовой многоугольник (или треугольник – если действуют три силы). При этом следует сначала сложить все заданные, а затем достроить неизвестные силы.
5. Решить силовой многоугольник (по известным элементам определить неизвестные) или, если силовой многоугольник построен в масштабе, определить искомые силы по масштабу.
При решении задач аналитическим способом рекомендуется придерживаться следующего порядка:
1. Выделить точку, равновесие которой надо рассмотреть.
2. Изобразить активные (заданные) силы.
3. Освободить точку от связей, приложив соответствующие реакции. При этом необходимо убедиться, что данная задача является статически определимой – число неизвестных величин должно быть не более двух или трех (в случаях плоской и пространственной систем сходящихся сил соответственно).
4. Направить оси координат.
5. Составить уравнения равновесия системы сходящихся сил, из которых можно найти неизвестные величины.
Пример. Стержни АС и ВС соединены между собой и с вертикальной стеной посредством шарниров (рис. 1.15). На шарнирный болт С действует вертикальная сила Р=1000 Н.
Определить реакции этих стержней на шарнирный болт С, если углы, составляемые стержнями со стеной, равны: α=30° и β=60°.
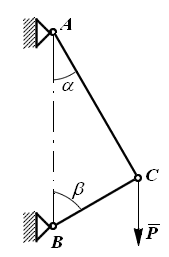
Рис. 1.15
Задачу можно решить либо аналитически, либо графически.
I. Геометрический способ. Очевидно, что объектом исследования в данной задаче является болт C, т.к. именно к нему приложены заданная сила 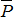 и стержни AC и BC, реакции которых нужно определить. Отбросим связи, заменив их действие реакциями.
и стержни AC и BC, реакции которых нужно определить. Отбросим связи, заменив их действие реакциями.
Построим замкнутый треугольник abc (рис. 1.16) для сил 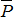 ,
, 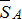 и
и 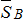 (т.к. болт C находится в равновесии), начав построение с известной силы
(т.к. болт C находится в равновесии), начав построение с известной силы 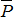 , которую изобразим вектором
, которую изобразим вектором 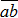 , тогда вектор
, тогда вектор 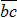 определит силу
определит силу 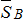 , а вектор
, а вектор 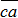 - силу
- силу 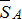 . При этом следует учесть, что известны только направления реакций связей.
. При этом следует учесть, что известны только направления реакций связей.
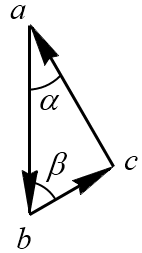
Рис. 1.16
Измерив отрезки 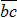 и
и 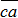 выбранной единицей масштаба, найдем величины неизвестных сил
выбранной единицей масштаба, найдем величины неизвестных сил 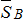 и
и 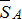 и задача будет графически решена.
и задача будет графически решена.
Величины неизвестных сил 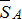 и
и 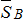 можно найти тригонометрически, решив силовой треугольник abc, т.е. в этом треугольнике известны сторона ab и два угла α и β.
можно найти тригонометрически, решив силовой треугольник abc, т.е. в этом треугольнике известны сторона ab и два угла α и β.
Итак, построим в масштабе вектор 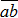 (который, как и
(который, как и 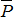 , направлен вертикально вниз) из точки a под углом α проведем одну линию, из точки b проведем вторую линию под углом β до пересечения их в точке с, треугольники ΔАВС и Δabc подобны.
, направлен вертикально вниз) из точки a под углом α проведем одну линию, из точки b проведем вторую линию под углом β до пересечения их в точке с, треугольники ΔАВС и Δabc подобны.
α+β=90° - по условию задачи, следовательно, Δabc – прямоугольный. Из этого треугольника находим:
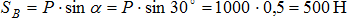
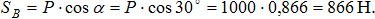
II. Аналитический способ. Выполним пункты 1-3 аналогично, как и при решении задачи графическим способом. Поэтому продолжим решение данной задачи с пункта 4 – выберем систему координат. Так как угол между неизвестными силами 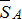 и
и 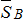 равен 90°, то удобнее всего направить по линиям действия этих сил оси координат.
равен 90°, то удобнее всего направить по линиям действия этих сил оси координат.
Направим Ох по линии действия 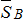 , а ось Оу – по линии действия
, а ось Оу – по линии действия 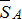 (рис. 1.17).
(рис. 1.17).
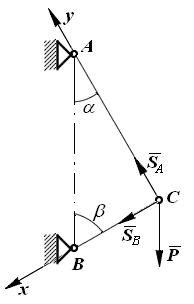
Рис. 1.17
Для данной плоской системы сходящихся сил составим 2 уравнения равновесия:
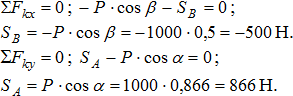
При аналитическом способе заранее неизвестно, в какую сторону направить реакции стрежней вдоль прямых АС и ВС. Если в результате решения получим положительные значения, то реакции были направлены верно, если получим отрицательные, то выбранное направление реакции изменим на противоположное.